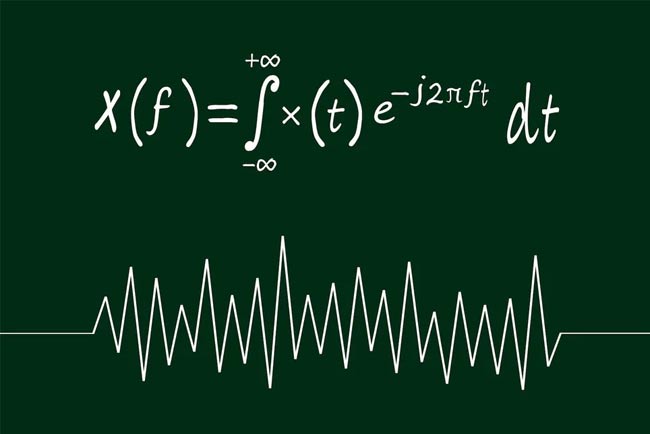با توسعه فناوری و ابزارهای محاسباتی پیشرفته، معادلات جدیدی نیز به وجود آمدهاند که به ما درک عمیقتری از جهان میدهند. الگوریتمهای هوش مصنوعی، مدلهای شبیهسازی پیچیده و روشهای ریاضی جدید، همگی به تحقیقات علمی و کاربردهای صنعتی کمک میکنند.
به گزارش ایتنا، چنین پیشرفتهایی در ریاضیات با توسعه درک ما از جهان همراه بودهاند. در این مقاله، نگاهی به نه معادله مهم تاریخ میاندازیم که نگاه ما به همه چیز از ذرات کوچک تا کیهان وسیع را تغییر دادهاند.
قضیه فیثاغورس
یکی از اولین قوانین مهم مثلثاتی که افراد در مدرسه یاد میگیرند، رابطه بین اضلاع یک مثلث قائمالزاویه است: جمع مجذور دو ضلع کوتاهتر برابر با مجذور ضلع بلندتر (وتر) است. این معادله به صورت a۲+b۲=c۲ نوشته میشود و دستکم ۳۷۰۰ سال پیش و از زمان بابلیان باستان شناخته شده است.
فیثاغورس این معادله را به شکل امروزی تدوین کرد. این قضیه در ساختوساز، ناوبری، نقشهکشی و فرآیندهای مهم دیگر کاربرد دارد و به گسترش مفهوم اعداد نیز کمک زیادی کرده است.
در واقع قضیه فیثاغورس با بیان رابطه بین اضلاع یک مثلث قائمالزاویه، نقش مهمی در مهندسی، معماری و ناوبری داشته است. در صنعت ساختمانسازی، از این قضیه برای محاسبه دقیق زاویهها و طولها استفاده میشود تا سازههایی استوار و مقاوم ایجاد شوند.
در فناوری نیز این قضیه به توسعه الگوریتمهای مختلف کمک میکند، به خصوص در گرافیک کامپیوتری و طراحی بازیهای ویدیویی که نیاز به محاسبات دقیق فواصل دارند. در زندگی روزمره نیز قضیه فیثاغورس به ما کمک میکند تا از مسافرتهای جادهای گرفته تا اندازهگیریهای روزمره در خانه و محل کار، مسافتهای مستقیم بین دو نقطه را محاسبه کنیم.
قانون دوم نیوتن (F=ma) و قانون جاذبه عمومی
سِر آیزاک نیوتن به کشفیات فراوان خود در عرصه ریاضیات و فیزیک شهرت دارد. یکی از مهمترین آنها قانون دوم حرکت است که بیان میکند نیرو برابر است با جرم جسم ضرب در شتاب آن که به صورت F=ma نوشته میشود.
به گزارش ایتنا، این قانون به همراه دیگر مشاهدات، نیوتن را در سال ۱۶۸۷ به توصیف قانون جاذبه عمومی سوق داد. این قانون به صورت F = G (m1 * m2) / r^2 نوشته میشود و برای درک بسیاری از سیستمهای فیزیکی از جمله حرکت سیارات در منظومه شمسی مورد استفاده قرار میگیرد.
قانون دوم نیوتن و قانون جاذبه عمومی ابزارهای بنیادی در فیزیک هستند که کاربردهای گستردهای در صنعت، فناوری و زندگی روزمره دارند. برای مثال، قانون دوم نیوتن در صنعت خودرو برای طراحی سیستمهای ایمنی خودروها مانند ترمزها و ایربگها استفاده میشود.
قانون جاذبه عمومی نیز در فناوری فضایی برای محاسبه مدارهای ماهوارهها و فضاپیماها به کار میرود. همچنین، این قوانین در زندگی روزمره به ما کمک میکنند تا حرکات اشیاء را بهتر درک کنیم و اقدامات لازم را برای جلوگیری از حوادث (مانند نگهداری ایمن اجسام سنگین و پیشبینی مسیر سقوط آنها) انجام دهیم.
معادله موج
در سال ۱۷۴۳ بود که ژان-باپتیست لورون دالامبر معادلهای را برای توصیف ارتعاشات یک رشته نوسانی یا حرکت موجی استخراج کرد. این معادله به صورت
1/v^2 * ∂^2y/∂t^2= ∂^2y/∂x^2 نوشته میشود و برای پیشبینی حرکت امواج آب، زلزله و صدا مورد استفاده قرار میگیرد.
معادله موج، ابزاری کلیدی برای تحلیل و پیشبینی رفتار موجها در محیطهای مختلف به شمار میرود. این معادله در صنعت مخابرات برای طراحی و بهینهسازی شبکههای ارتباطی استفاده میشود، به خصوص در انتقال امواج رادیویی و سیگنالهای اینترنتی.
در فناوری صوتی، معادله موج برای بهبود کیفیت صدا در دستگاههای صوتی و سیستمهای صوتی حرفهای بهکار میرود. در زندگی روزمره، این معادله به درک بهتر از رفتار موجها در آب، هوا و حتی امواج زلزله کمک میکند و میتواند در برنامهریزیهای ایمنی و بهبود سیستمهای هشدار دهنده کاملاً مؤثر باشد.
معادلات فوریه
حتی اگر نام بارون فرانسوی ژان باپتیست ژوزف فوریه را نشنیده باشید، اما کارهای علمی او به طور حتم زندگی شما را تحت تاثیر قرار دادهاند. معادلات ریاضی که او در سال ۱۸۲۲ نوشت، به محققان این امکان را داده است که دادههای پیچیده و آشفته را به ترکیبی از امواج ساده تجزیه کنند که تحلیل آنها بسیار آسانتر است.
به گزارش ایتنا، گفتنی است تبدیل فوریه در زمان خود یک مفهوم رادیکال بود و بسیاری از دانشمندان فکر نمیکردند که سیستمهای پیچیده را بتوان به معادلاتی چنین ساده فرو کاهید. امروزه تبدیلهای فوریه در بسیاری از زمینههای مدرن علوم، از جمله پردازش دادهها، تجزیه و تحلیل تصویر، اپتیک، ارتباطات، نجوم و مهندسی مورد استفاده قرار میگیرند.
معادلات فوریه با تجزیه و تحلیل دادههای پیچیده به امواج ساده، کاربردهای فراوانی در صنعت، فناوری و زندگی روزمره دارند. برای مثال، این معادلات در صنعت برای تحلیل ارتعاشات و نویز در ماشینآلات و تجهیزات استفاده میشوند تا عملکرد بهینه و عمر طولانیتری داشته باشند.
در عرصه فناوری نیز معادلات فوریه در پردازش سیگنالهای دیجیتال، از جمله تصاویر، صداها و دادههای پزشکی، نقش حیاتی ایفا میکنند. همچنین در زندگی روزمره، از این معادلات در برنامههای کاربردی موسیقی، بهبود کیفیت تصاویر و فیلمها و حتی در بهینهسازی مصرف انرژی در خانهها و ساختمانها استفاده میشود.
معادلات ماکسول
در سال ۱۸۶۴ جیمز کلرک ماکسول فهرستی از ۲۰ معادله را منتشر کرد که چگونگی عملکرد و ارتباط الکتریسیته و مغناطیس را توضیح میدادند. این معادلات در قالب چهار معادله اساسی خلاصه میشود که پایهای برای الکترونیک در دنیای مدرن ما تشکیل میدهند.
معادلات ماکسول که به شرح و تبیین بنیاد الکترومغناطیس میپردازند، تاثیرات گستردهای در صنعت، فناوری و زندگی روزمره دارند. این معادلات در صنعت برای طراحی و بهینهسازی موتورهای الکتریکی، ژنراتورها و ترانسفورماتورها استفاده میشوند.
در بخش فناوری نیز معادلات ماکسول به توسعه دستگاههای ارتباطی بیسیم، از جمله تلفنهای همراه، وایفای و رادارها کمک میکنند. از سوی دیگر، این معادلات در زندگی روزمره در کاربردهایی مانند مایکروویوها، تلویزیونها و سایر دستگاههای الکترونیکی که وابسته به امواج الکترومغناطیسی هستند، مورد استفاده قرار گرفته و به بهبود کیفیت و کارایی آنها کمک میکنند.
معادله مشهور E=mc2
معادله معروف E=Mc۲ که نخستینبار توسط آلبرت انیشتین در سال ۱۹۰۵ کشف و بیان شد، نشان میدهد که ماده و انرژی اصطلاحاً دو روی یک سکه هستند.
ما بدون این معادله نمیتوانستیم به عملکرد ستارگان یا کیهان پی ببریم. این معادله مشهور آلبرت انیشتین نقش مهمی در درک انرژی و ماده دارد و تاثیرات گستردهای در صنعت، فناوری و زندگی روزمره داشته است.
برای مثال، از این معادله در صنعت هستهای برای محاسبه انرژی آزادشده در واکنشهای هستهای استفاده میشود که نتیجه آن، تولید انرژی در نیروگاههای هستهای و همچنین توسعه سلاحهای هستهای بوده است.
این معادله در حوزه فناوری نیز به پژوهشهای پیشرفته در فیزیک ذرات و شتابدهندههای ذرات کمک شایانی کرده است. همچنین، مفاهیم این معادله در زندگی روزمره و در فناوریهای پزشکی مانند PET برای تشخیص بیماریها به کار میرود و به درک بهتر از کیهان و انرژیهای عظیم موجود در آن کمک میکند.
معادلات فریدمن
در دهه ۱۹۲۰، فیزیکدان روسی الکساندر فریدمن با استفاده از نظریههای نسبیت انیشتین نشان داد که ویژگیهای یک جهان در حال انبساط از مهبانگ به بعد را، میتوان با دو معادله بیان کرد. این معادلات همه جنبههای مهم کیهان را ترکیب میکنند و برای درک انبساط شتابدار جهان استفاده میشوند.
به گزارش ایتنا، معادلات فریدمن به توضیح انبساط کیهانی و دینامیک جهان کمک میکنند و کاربردهای مهمی در کیهانشناسی، صنعت و فناوری دارند. این معادلات در کیهانشناسی برای مدلسازی انبساط جهان و پیشبینی آینده آن مورد استفاده قرار میگیرند.
در بخش صنعت نیز مفاهیم این معادلات به توسعه فناوریهای مرتبط با فضا مانند ماهوارهها و تلسکوپهای فضایی کمک کردهاند. همچنین درک این معادلات در زندگی روزمره، به توسعه دانش عمومی درباره منشأ و تکامل جهان کمک کرده و الهامبخش مطالعات بیشتر در علوم پایه و آموزش بودهاند.
معادله اطلاعات شانون
در سال ۱۹۴۸، کلود شانون (ریاضیدان و مهندس آمریکایی) در یک مقاله، معادلهای برای نشان دادن حداکثر کارایی انتقال اطلاعات معرفی کرد. این معادله به صورت C = B * 2log(1+S/N) نوشته میشود و در واحدهای بیت در ثانیه خروجی دارد.
معادله اطلاعات شانون اساس نظریه اطلاعات را تشکیل میدهد و تاثیرات بزرگی در صنعت، فناوری و زندگی روزمره داشته است. به عنوان نمونه، این معادله در صنعت مخابرات برای بهینهسازی کدینگ و انتقال دادهها استفاده میشود تا اتلاف اطلاعات به حداقل برسد.
معادله شانون در فناوری نیز به توسعه الگوریتمهای فشردهسازی دادهها مانند JPEG و MP3 کمک کرده است که در کاهش حجم فایلها و بهبود کیفیت آنها تا حد بسیار زیادی موثر هستند. علاوه بر این، این معادله در زندگی روزمره نیز در بهبود کارایی شبکههای اینترنتی و سرعت انتقال دادهها نقش دارد و تجربه کاربری بهتری را در ارتباطات دیجیتال فراهم میکنند.
نقشه لجستیک می
رابرت می (فیزیکدان، ریاضیدان و اکولوژیست استرالیایی) در سال ۱۹۷۶ در مقالهای که در نشریه Nature منتشر شد، به معرفی معادله xn+1 = k * xn(1 – xn) پرداخت. این معادله با وجود سادگی، نتایج بسیار پیچیدهای در بر دارد و برای توضیح دینامیک جمعیت در سیستمهای اکولوژیکی و تولید اعداد تصادفی برای برنامهنویسی کامپیوتری استفاده میشود.
نقشه لجستیک می در بخش صنعت، برای تحلیل پایداری و تغییرات جمعیت در اکوسیستمها و سیستمهای تولیدی استفاده میشود. در حوزه فناوری نیز نقشه لجستیک می برای شبیهسازی و پیشبینی رفتارهای پیچیده در شبکههای اجتماعی و سیستمهای اقتصادی به کار میرود.
به گزارش ایتنا، معادلات ریاضی که در اینجا بررسی شدند، نه تنها درک ما از جهان را تغییر دادهاند بلکه کاربردهای عملی و عملی فراوانی نیز دارند. همانطور که دیدیم، از ساختوساز و ناوبری گرفته تا پردازش دادهها و پیشبینیهای علمی، این معادلات بهطور گستردهای در علوم و فناوری استفاده میشوند.
ما با استفاده از این معادلات میتوانیم به درک بهتری از دنیای پیرامون خود برسیم و راهحلهایی برای چالشهای پیچیده پیدا کنیم. معادلاتی که در این مقاله بررسی شد، تنها نقطه شروعی برای این سفر بیپایان علمی هستند.

 دریافت لینک صفحه با کد QR
دریافت لینک صفحه با کد QR